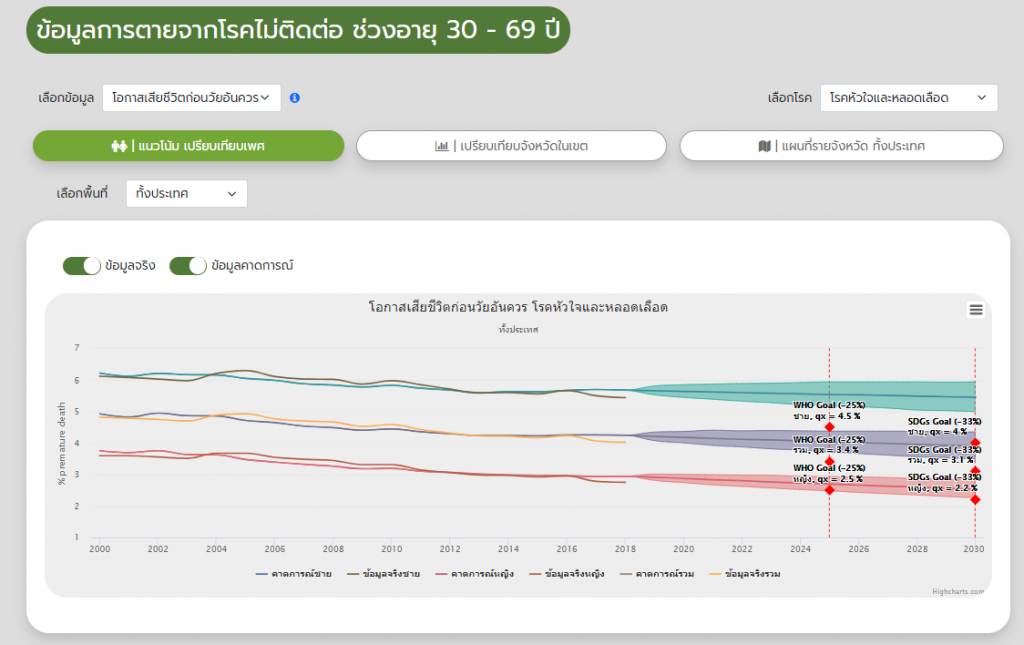
สถานการณ์โอกาสของการเสียชีวิตก่อนวัยอันควร (premature death) ของประชากรไทยช่วงอายุ 30-69 ปีของกลุ่มโรคไม่ติดต่อ 4 กลุ่มโรค ได้แก่ โรคหัวใจและหลอดเลือด โรคมะเร็ง โรคเบาหวาน และโรคที่เกี่ยวกับระบบทางเดินหายใจเรื้อรัง พ.ศ. 2543-2561 และพยากรณ์ค่าไปถึง พ.ศ. 2573 (ตามเป้าของ SDGs) และ พ.ศ. 2568 (ตามเป้าของสำนักโรคไม่ติดต่อและ WHO)
ข้อมูลที่ใช้ในการศึกษา
ข้อมูลการตาย: ใช้ข้อมูลการตายจากสำนักบริหารการทะเบียน กรมการปกครอง กระทรวงมหาดไทย พ.ศ. 2543-2561 ซึ่งบันทึกรหัสสาเหตุการตายโดยกองยุทธศาสตร์และแผนงาน กระทรวงสาธารณสุข จำแนกการตายตามอายุและเพศของกลุ่มโรคไม่ติดต่อ 4 กลุ่มโรค ประกอบด้วยกลุ่มโรคหัวใจและหลอดเลือด (cardiovascular diseases: I00-I99) โรคเกี่ยวกับการหายใจเรื้อรัง (chronic respiratory diseases: J30-J98) มะเร็ง (cancer: C00-C97) และเบาหวาน (diabetes: E10-E14) ซึ่งบันทึกสาเหตุการตายตามรายการโรคจากโรคของบัญชีจำแนกโรคระหว่างประเทศฉบับที่ 10 (International Classification of Diseases : ICD-10) ที่จัดโดยมีการปรับสาเหตุการตายจากมรณบัตรด้วยผลการศึกษาสาเหตุการตายโดยการสัมภาษณ์และทบทวนเวชระเบียนที่ศึกษาล่าสุด (พ.ศ. 2548)
ข้อมูลประชากร: ใช้ข้อมูลประชากรกลางปีที่จัดทำโดยกองยุทธศาสตร์และแผนงาน ซึ่งเป็นข้อมูลจากสำนักบริหารการทะเบียน กรมการปกครอง กระทรวงมหาดไทยที่จำแนกรายอายุและเพศ พ.ศ. 2543-2561
การวิเคราะห์ข้อมูล
การตายก่อนวัยอันควร (premature death) วัดด้วยความน่าจะเป็นของการตาย (probability of dying: qx) คือ โอกาสที่คนคนนึงสามารถมีชีวิตอยู่ได้ตั้งแต่เกิดจนตาย โดยคิดจากการประมาณอัตราการเสียชีวิต (death rate) ด้วยการหาค่าเฉลี่ยความเสี่ยงเฉพาะอายุ (age-specific risk)

การพยากรณ์การเสียชีวิตก่อนวัยอันควรในการศึกษานี้ใช้วิธี Bayesian model averaging (BMA) ตามการศึกษาของ Kontis et. Al. (2017)[1] โดยเป็นการพยากรณ์ค่าอัตราตายรายอายุ (age-specific mortality) ซึ่งนำไปใช้ในการคำนวณต่อเพื่อหาค่าความน่าจะเป็นของการตาย (probability of dying) ซึ่ง BMA จะใช้ 2 โมเดล คือ Age-time models และ Lee-Carter models การวิเคราะห์ข้อมูลเราใช้ R software (version 3.6.1) ในการพยากรณ์ค่าโมเดลโดยการสุ่มซ้ำ (sampling draws) 1,000 ครั้ง จากการประมาณค่าเฉลี่ย (mean) และค่าความแปรปรวน (variance) ซึ่งจะได้ posterior distribution ของอัตราตายรายอายุ (age-specific death rates) ตามสัดส่วนน้ำหนักของแต่ละโมเดล และสุดท้ายจะรวมได้ posterior distribution ของ age-specific death rates ภายใต้ BMA สำหรับใช้ในการพยากรณ์
—————————————————————————————————————————-
[1] Kontis V, Bennett JE, Mathers CD, Guangquan Li, Foreman K, Ezzati M. Future life expectancy in 35 industrialised countries: projections with a Bayesian model ensemble. Lancet. 2017;389:1323-35.